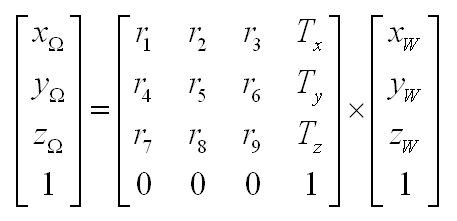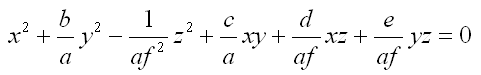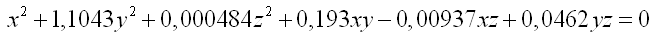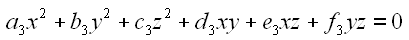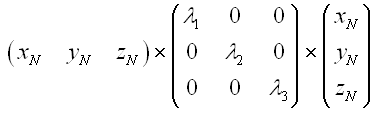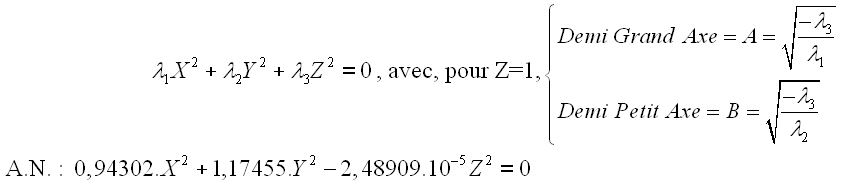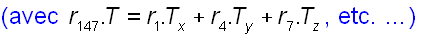La
souris oculaire
|
Lorsqu'on
travaille sur
écran
d'ordinateur,
- on
cherche des yeux la zone de l'écran qui nous
intéresse,
- puis
on bouge le bras pour amener la souris sur la zone visée,
- puis
on clique sur cette zone.
Si
on travaillait avec un
vrai ordinateur, comme dans les films,
- on
regarderait un point de l'écran
- et
la souris viendrait se positionner toute seule sur ce point.
La
souris oculaire, c'est quand l'oeil positionne la souris.
|
|
Comment
un ordinateur pourrait deviner le point de l'écran que je
regarde ?
Il
faudrait qu'il puisse me regarder,
regarder mes yeux,
avec une caméra !
On fait toujours ça, nous, quand on discute avec quelqu'un : on
regarde ses yeux, et on sait où il
regarde !
On
trouve, sur le marché, des dispositifs
opérationnels, mais à des prix exorbitants
- soit
pour les handicapés
- soit
pour les pilotes d'avion de combat ou
autres besoins très ciblés.
Aucune
solution pour un utilisateur de base.
Les
yeux sont mobiles, rapides, bien visibles.
Comment les utiliser pour communiquer avec
l'ordinateur ?
Au
départ, voici 10 ans, nous avons cherché
à
résoudre la totalité du
problème.
Nous
avons créé un outil de laboratoire,
délicat, qui nous a
permis d'avancer.
Merci
à Pierre Christiaen, Vincent Royal et
Dominique Szymik !
Un certain nombre de problèmes techniques ont
été résolus, des choix de base ont
été faits :
- La tête de
l'utilisateur doit rester libre (à l'intérieur
d'un volume donné)
- Eclairage par infrarouge,
et donc travail en noir et blanc.
- Deux caméras,
pour obtenir l'information "distance"
- Caméras en
position basse, pour que la pupille soit moins souvent
cachée par la paupière.
- Pas de technique de
reflets cornéens : ce serait mieux, mais cela impose trop de
contraintes.
Un
certain nombre de problèmes ont été
provisoirement écartés :
- Utilisation de
caméras mobiles : plus tard !
- Comment
éclairer le visage pour bien voir la pupille.
- Comment trouver une
petite pupille dans une grande image.
- Comment corriger l'effet
de loupe de la cornée.
- Problème des
porteurs de lunettes.
- Quel oeil analyser
(comment détecter l'oeil directeur)
- Comment cliquer ?
La question
intéressante, dans ce problème,
c'est :
La caméra donne
une image
où je vois une pupille.
Comment, à partir
de cette image, retrouver le point de
l’écran visé par
l’œil ?
C’est
l’objet principal de ce document.
Maintenant, pourquoi notre système n'est pas encore vendu
dans les hypermarchés ?
C'est
l'objet de la fin de ce document.
Le
problème
principal est donc celui-ci :
Soit
une image de 500 pixels (en horizontal) sur 255 pixels (en
vertical). On
y trouve une petite ellipse
Ceci est
effectivement
obtenu avec une bonne intensité lumineuse et les
réglages adaptés. |
 |
Que
peut-on en déduire ?
La forme et la position de l'ellipse
donnent presque toutes les informations.
Le
principe du calcul.
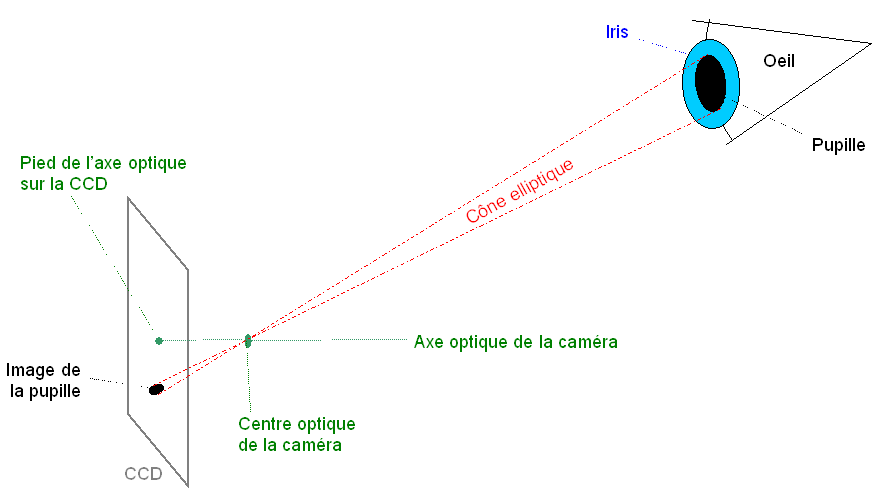
Voici
le schéma global.
Le
coeur du calcul va consister à
- Trouver
l'équation de l'image de la pupille, sur la CCD.
- En
déduire l'équation du cône elliptique.
- Trouver
un cercle inscrit dans le cône elliptique
En
fait, pour une position donnée de l'oeil, on trouve 2
cercles possibles (par raison de symétrie).
On trouve un truc pour sélectionner la solution
répondant au problème.
Il reste à trouver un dernier truc pour
déterminer la position de l'oeil, et c'est (presque) fini. |
On suppose
que les rayons lumineux traversent le centre
optique
suivant une ligne droite.
Il ne sera pas compliqué
d'apporter le terme
correctif quand il le faudra.
Etape
préliminaire : Calibrage de la caméra.
Avant
de commencer, il faut avoir calibré
la caméra.
Voici
ce que cela
signifie :
Il
y a l’espace dans lequel nous évoluons,
ramené à un
référentiel noté W (World).
-
On y a défini une origine W, les 3 axes Wx, Wy
et Wz.
-
Chaque point de notre espace peut être localisé
par ses 3 coordonnées,
x, y et z.
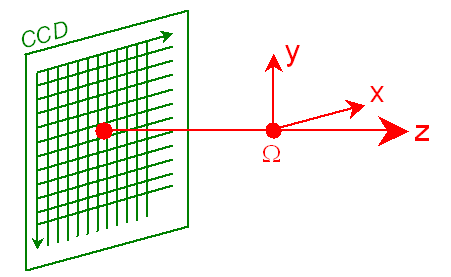
Dans
notre cas de souris
oculaire, on choisit un référentiel W
lié
à l’écran (cf. schéma)
|
|
Il
y a l'espace "Caméra" qui a sa propre organisation :
- La
caméra a un axe optique : c'est
l'axe optique du jeu de lentilles de l'objectif.
- Sur
l'axe optique est situé le Centre optique,Ω,
quelque part à l'intérieur des lentilles.
- Perpendiculaire
à l'axe optique, à l'intérieur de la
caméra, on a le plan de la CCD, qui enregistrera l'image.
- Ce
plan est constitué d'un damier de cellules CCD, physiquement
rangées en horizontal et en vertical.
Le
référentiel Caméra sera tout
naturellement organisé ainsi :
- Origine
: Ω,
centre optique.
- Axes
Ωx
et Ωy
: respectivement parallèles aux
rangées
horizontales et verticales des cellules CCD
- Axe
Ωz
: c'est l'axe optique de la caméra
|
Problème
: je connais un
point (ses 3 coordonnées) dans le
référentiel W.
Quelles sont ses coordonnées dans
le
référentiel Ω
?
Et inversement : je connais un point de Ω
; quelles sont ses coordonnées dans W ?
Heureusement nous ne sommes pas les premiers à rencontrer le
problème,
et nos
prédécesseurs ont mis
au point
plusieurs techniques du Calibrage de caméras.
Nous
avons
suivi la technique de Tsaï (explications et logiciel
disponibles sur Internet).
La mise au point du banc de calibrage nécessite un
matériel haut de gamme,
ou plus
prosaïquement une
patience
à toute épreuve.
Il faut fabriquer une mire (une simple matrice de points,
imprimée
sur imprimante laser, suffit)
Cette mire doit être photographiée en deux
positions différentes, A et B, non
parallèles.
Chaque point de la mire nécessite la saisie de 10 nombres :
- les 3
coordonnées de chaque point dans l'espace W en position A et
en position B.
- les 2
coordonnées "pixel" de l'image du point ("pixels"
à virgule !) en position A et en
position B.
Cela
ne se fait pas en 10 minutes.
Et surtout, quand c'est fini, on ne bouge plus la caméra
tant le calibrage (artisanal) est une opération
démente.
Il faut reconnaître qu'après calibrage, on peut
effectuer
des mesures avec une précision époustouflante !
Dans
notre cas, le calibrage a renvoyé :
- 10
paramètres
« intrinsèques »
(géométrie
interne de la caméra)
- et
12 paramètres
« extrinsèques »
(comment passer
des coordonnées W aux coordonnées Ω de la caméra).
| Table
1 : Paramètres intrinsèques : |
Table
2 : Paramètres extrinsèques : |
Ncx
= 500
nbre de capteurs
sur une ligne
Nfx = 500
nbre de
pixels sur une ligne
dx
=
0.009315 mm largeur pixel
dy
=
-0.01260000 mm hauteur pixel ; signe
pour
référentiel direct
dpx
=
0.00980000 mm largeur pixel effective
dpy
=
0.01260000 mm hauteur pixel effective
Cx =
246.95929665 pix
abscisse pixel de W’, centre optique de la CCD
Cy =
128.18030740 pix
ordonnée pixel de W’, centre optique de la CCD
f
=
28.74428022 mm distance focale de
l’objectif
kappa1 =
-0.00000306 coefficient
de correction de lentille 1er degré
|
Tx
= 90.32921716 mm
vecteur de translation
Ty
= 47.03282722 mm entre
World et Oméga
Tz
= -215.03563304 mm
r1 = +0.98316820
matrice 3x3 de
rotation
r2
= -0.07248719 pour
passer de W
à Oméga
r3
= -0.16770777
r4
= +0.00931638
r5
= +0.93662334
r6
= -0.35021412
r7
= 0.18246505
r8
= 0.34275696
r9
= 0.92153360 |
Il
est clair que ces paramètres n'ont de valeur que dans notre
configuration
Ils
sont donnés pour permettre d'accompagner
numériquement le traitement présenté.
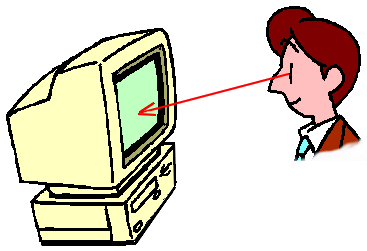
Pour passer des coordonnées W aux
coordonnées Ω,
voici la formule
:
(il s'agit d'une rotation, suivie d'une translation)
Les coordonnées
homogènes donnent le même résultat en
un produit unique :
- Les
paramètres intrinsèques restent valides
même la caméra change de position.
- Les
paramètres extrinsèques ne sont plus valides si
la
caméra change de position.
Géométrie
de la pupille : une ellipse.
Le
pourtour :
Une fois le calibrage de la caméra effectué, on
peut retourner à
l'image de l’ellipse :
Coordonnées des points de pourtour de l’ellipse.
| |
Chaque
point du pourtour de l’ellipse est
repéré par ses 2 coordonnées :
x-pixel et y-pixel
Les
pixels n’étant pas carrés, il faut
convertir les coordonnées en millimètres.
L'origine
des axes n'est pas le pixel en haut à gauche mais Ω’,
pied de l'axe optique sur la CCD.
(le constructeur de la caméra
ne peut pas
garantir
que
l’axe optique de la
caméra passe par le centre
géométrique de la CCD.
La
position de Ω a
été déterminée lors du
calibrage.)
D'où
un premier changement de repères.
|
Changement
de repères : Pixels vers Ω’.
(les diverses variables proviennent du calibrage)
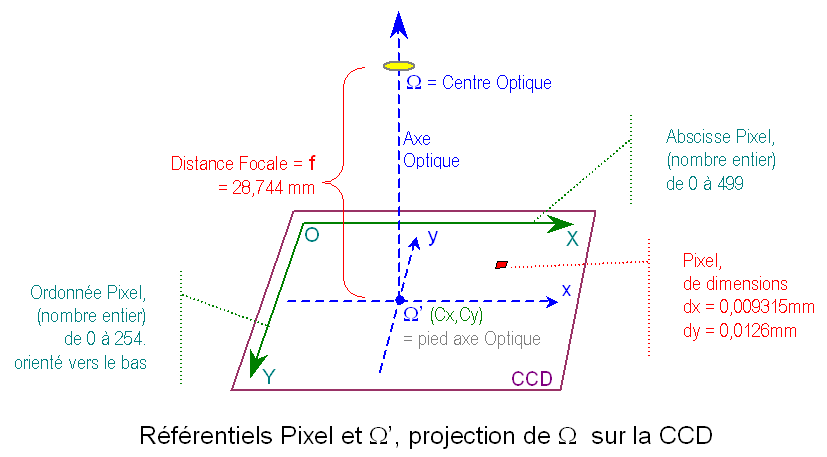
 Schéma
: Référentiels Pixels et Ω’
orthonormé.
Schéma
: Référentiels Pixels et Ω’
orthonormé.
Chaque point du pourtour de l'ellipse peut donc être
exprimé dans le référentiel Ω’.
On suppose ici que la caméra est de type
"Sténopé" : les rayons lumineux traversent le
centre optique en ligne droite.
En pratique, l'objectif utilisé peut
nécessiter un ou plusieurs termes correctifs (variable kappa1 dans
Tsaï).
Si c'était le cas, il faudrait ici
créer une image corrigée de la CCD avant de
passer à la suite.
L'équation
de l'ellipse.
Connaissant
les points du pourtour de l'ellipse,
quelle est l'équation
de l'ellipse qui coïncide au mieux avec l'ellipse
visible ?
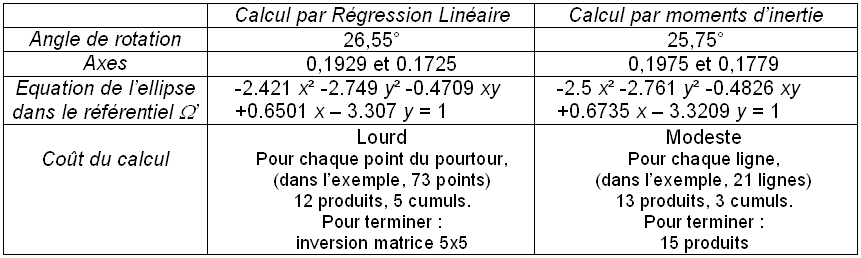
Deux méthodes sont possibles : (voir
détails)
- méthode
par "régression linéaire".
- méthode
par moments d'inertie.
Voici
les résultats pour chaque méthode :
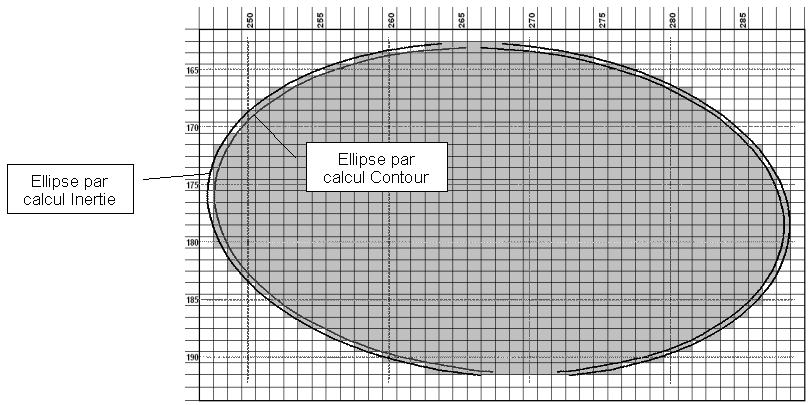
et
les ellipses en résultant :
Par la
suite, nous aurons l'occasion de constater que la technique par
inertie est plus robuste.
Nous
continuons ici avec les résultats fournis par cette
méthode.
Le
cône elliptique.
Il
faut maintenant travailler dans l'espace ;
Les points du pourtour de la pupille (réelle) et le centre
optique de la caméra forment un cône
elliptique.
Ce cône trace sur la CCD le pourtour de l'image de la pupille.
Cette équation du cône elliptique donne
une information importante, car le pourtour de la
pupille
(réelle) appartient à ce cône. |
 |
On passe ainsi d'une équation dans l'autre :
| Equation
de l'ellipse dans le plan de la CCD |
|
Equation
du cône elliptique dans le référentiel Ω |
 |
 |
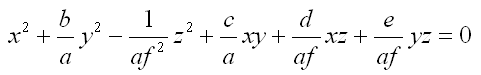 |
Application
numérique :
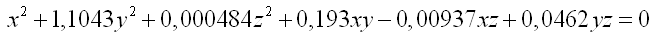
On est un peu déçu : on aurait
rêvé de trouver une formule qui
évoquait mieux l'ellipse :
ax² +
by² = constante
En
fait, cette formule du cône elliptique est donnée
dans un référentiel qui n'est pas
l'idéal pour le cône elliptique.
On voudrait changer une nouvelle fois de
référentiel, pour obtenir une équation
"normalisée"
A
l'époque où il y avait moins d'un ordinateur par
km², ce problème avait une belle solution
théorique :
Diagonalisation de matrices par "Valeurs
propres" et "Vecteurs propres".
Maintenant, cette solution théorique est devenue une
technique banale
L'équation
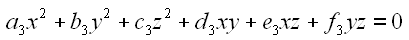
peut
s'écrire ainsi :

Dans
l'espace "normalisé" cherché, cette
équation deviendra :
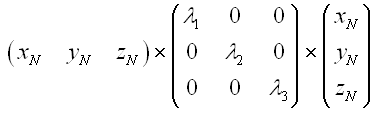
La
diagonalisation de la matrice de l’équation de
départ va fournir :
- les trois
valeurs propres λ1, λ2 et λ3 ,
- les
trois vecteurs propres ({V1x,
V1y, V1z}, {V2x,
V2y, V2z},
{V3x, V3y, V3z})
donnant la matrice de
passage.
Voir le
détail
de ces transformations.
En résumé :

Equation du
cône dans le référentiel N :
Orientation
du cercle générateur
On connait
maintenant l'équation du cône elliptique dans un
référentiel clairement identifié.
On se souvient que la pupille (réelle) est un cercle
directeur
de ce cône (le cône s'appuie sur le contour de la
pupille)
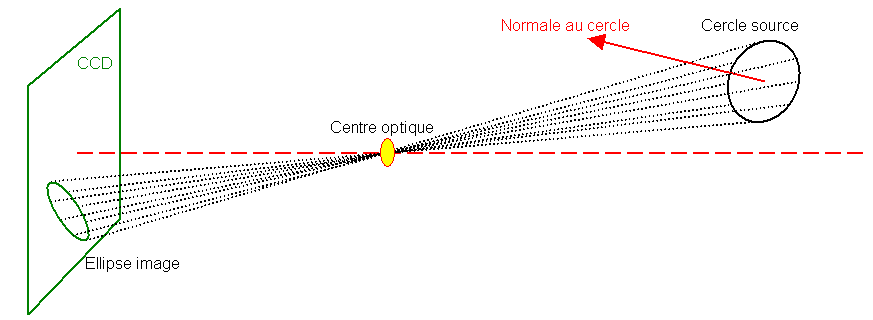
Pour mieux
comprendre la suite, supposons un cône sphérique
positionné verticalement, et une pièce de monnaie.
La pièce de monnaie tombe dans le cône :
Au fur et à mesure que la pièce descend, les
parois se resserrent.
A chaque niveau du cône, le plan horizontal forme une ellipse.
La pièce sera bloquée lorsque son
diamètre deviendra égal au grand
diamètre de l'ellipse.
La pièce pourra ensuite pivoter et venir
toucher la paroi de l'ellipse. Il y aura deux positions limites.
Dans ces positions limites, la pièce
devient "Cercle directeur". |
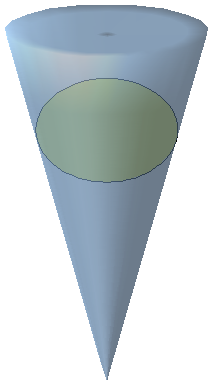 |
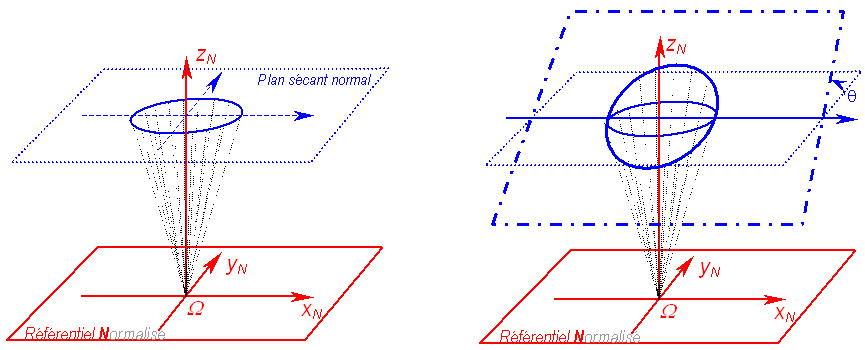
Nous
cherchons d’abord un cercle directeur. Nous
nous situons dans le plan perpendiculaire à l’axe ΩzN,
situé à une distance unitaire du centre
optique Ω. Nous utilisons alors le grand axe
de l’ellipse
comme charnière. Il arrive un moment où le plan
sécant coupe le cône selon un
cercle.
Dans le plan yNΩzN ,
cela se traduit ainsi :
(avec
l'hypothèse où ΩM = 1)
PQ est le petit axe initial ;
la droite PQ pivote autour de M pour donner P'Q'.
On arrête la rotation lorsque le petit axe P'Q' devient
égal au grand axe de l'ellipse.
Soit
M', le milieu de P'Q' ; dès que P'Q' n'est plus confondu
avec PQ, M' n'est plus confondu avec M.
En conséquence le grand axe de l'ellipse
découpée
dans le cône par le plan pivotant n'est plus le grand axe
initial. |
 |
Voici une façon de mener le calcul :
Discussion
sur le résultat.
Nous
sommes parti avec l'hypothèse d'une charnière
située à une distance unité
de Ω.
Toutes les solutions obtenues par homothétie de
centre Ω
sont également acceptables.
Les vecteurs directeurs de toutes les solutions
homothétiques sont identiques.
Il y a deux familles de solutions symétriques :
celle
obtenue
avec l'angle θ positif, et celle obtenue avec θ
négatif.
Pour lever l'ambiguïté de la symétrie,
il faut faire appel à des solutions externes.
Dans notre application d'origine, le cercle est une pupille ;
La caméra est située en contrebas, et la pupille
regarde plus haut que la caméra.
Le haut de la pupille est donc plus éloigné de la
caméra que le bas de la pupille.
On choisit donc un pixel du pourtour sur la partie haute de l'ellipse.
On calcule les coordonnées de ce point dans les
différents référentiels (Ω',
puis Ω
et enfin N)
Dans ce référentiel N, c'est sa
coordonnée yN
qui va apporter la solution.
Si
cette coordonnée est positive, on sera dans le cas A.
Si cette coordonnée est négative, on sera dans le
cas B.
Report des
informations dans le référentiel W(orld)
Les
informations précédentes sont connues dans le
référentiel Normalisé.
Il reste à les reporter dans le
référentiel absolu.
Voici les matrices de passage :
Ces calculs
sont-ils corrects ?
Pour
valider ces calculs, nous avons effectué des simulations :
- Nous
avons créé une pupille virtuelle.
- Nous
l'avons placée (virtuellement) dans
le champ de vision de la caméra,
à 50 cm de la caméra.
- Nous
avons quadrillé l'écran (24 lignes, 32 colonnes,
soit 768
noeuds répartis régulièrement sur la
surface de
l'écran)
- Nous
avons fait fixer (virtuellement) la pupille sur chacun de ces 768
points.
- A
chaque fois, nous avons recréé l'image de la
pupille sur la CCD.
- Nous
avons ensuite analysé l'image et
vérifié que nous
retombons bien sur le point d'écran virtuellement
visé.
Les
résultats sont décevants : ils sont visibles ici.
Oublions
les résultats issus des calculs de l'équation de
l'ellipse par régression :
La technique par inertie est incomparablement meilleure !
Voici
deux résultats intéressants :
- le
premier pour une pupille de 4 mm de diamètre, ce qui
correspond
à peu près à la
réalité.
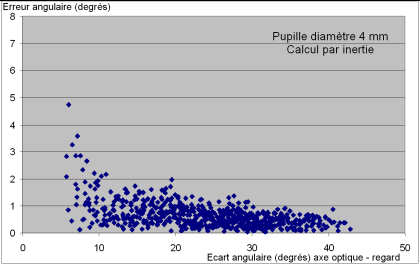
- le
second avec une pupille énorme (16 mm), pour voir !
Ces
résultats se lisent ainsi :
|
|
En
abscisse, quel est l'angle (en degrés) entre le regard vers
la
caméra et le regard vers le point
désigné de
l'écran ;
les résultats sont catastrophiques quand cet angle devient
petit : l'ellipse devient un cercle !
En ordonnée, quel est l'angle (en degrés) entre
le regard
vers le point théorique et le regard vers le point
calculé ;
les résultats, pour la pupille raisonnable de
diamètre 4 mm, sont vraiment tristes ! |
- Première
conclusion : il faudra 2 caméras, et basculer sur la
caméra la plus éloignée du regard.
(Résultat intéressant : avec 2
caméras, il sera possible d'évaluer la distance
caméra-oeil)
- Seconde
conclusion : le matériel mis en place est
inadéquat.
Ce
matériel, conçu voici 10 ans, permettait de
capter l'image binaire de la pupille (blanc ou noir), dans un rectangle
d'environ 40 sur 30 pixels.
Le
dernier graphique correspond à une capture de pupille dans
un
rectangle d'environ 160 sur 120 pixels, et le
résultat devient
satisfaisant.
D'où la solution simpliste : attendre
l'arrivée de caméras de 2500 pixels.
On peut tenter de contourner la difficulté :
Le
bruit, évident sur les graphiques, est un bruit de
binarisation :
si un
pixel noir devient pixel blanc, le point du regard calculé
se décale
sensiblement.
La solution est de prendre en compte, en niveaux de gris, les pixels en
périphérie de la pupille.
- Notre
matériel ne sait pas le faire : il binarise automatiquement.
- Actuellement,
le matériel commercialisé peut le faire, sans
problème.
|